Are Bits In Trivium Registers Shifting Right

Abstract

In this paper, nosotros propose a central-recovery assail on Trivium reduced to 855 rounds. As the output is a complex Boolean polynomial over hush-hush key and IV bits and information technology is difficult to observe the solution of the secret keys, nosotros propose a novel nullification technique of the Boolean polynomial to reduce the output Boolean polynomial of 855-circular Trivium. Then nosotros determine the degree upper jump of the reduced nonlinear boolean polynomial and discover the right keys. These techniques tin can be applicative to most stream ciphers based on nonlinear feedback shift registers (NFSR). Our assault on 855-round Trivium costs time complication $2^{77}$. Equally far as nosotros know, this is the best key-recovery assail on round-reduced Trivium. To verify our attack, we too give some experimental data on 721-round reduced Trivium.

Keywords

Trivium
Nullification technique
Polynomial reduction
Iv representation
Cardinal-recovery attack

1 Introduction

Almost symmetric cryptographic primitives can be described by boolean functions over surreptitious variables and public variables. The secret variables are often key bits, the public variables are oftentimes plaintext bits for block ciphers and Iv bits for stream ciphers. The ANF (algebraic normal form) representation of the output is usually very complex by repeatedly executing a uncomplicated iterative function, where the iterative office is a round function for block ciphers or a feedback office for stream ciphers based on nonlinear feedback shift registers. For stream ciphers, obtaining the exact output boolean functions is usually impossible. But if its degree is low, the nil tin can not resist on many known attacks, such equally higher order differential attacks [13, 15], cube attacks [1, 4], and integral attacks [14]. Hence, it is important to reduce the degree of polynomials for cryptanalysis of stream ciphers.

Trivium, based on a nonlinear feedback shift annals (NFSR), is ane of the finalists by eSTREAM projection and has been accepted as ISO standard [2, ten]. Trivium has a simple structure, with just bit operations, so that it can be applicative to source restricted applications such as RFID. By iteratively using NFSR, the degree increases quickly and the output is a complex boolean office over key and IV $.25.

There take been lots of cryptanalysis of Trivium since its submission. The early results include the chosen 4 statistical attack [vi, seven], which was applied to key-recovery attack on Trivium reduced to 672 rounds. Inspired past the message modification technique [twenty, 21], Knellwolf et al. invented the conditional differential tool [11], which was applicable to distinguishing stream ciphers based on NFSR. In [12], Knellwolf et al. proposed a distinguishing attack on 961-round Trivium with practical complication for weak keys.

Cube attacks are the major methods for recent cryptanalysis results of reduced round Trivium. In [4], Dinur and Shamir proposed a practical full key recovery on Trivium reduced to 767 rounds, using cube attacks. Later, Aumasson et al. [one] provided the distinguishers of 790-round Trivium with complexity $2^{30}$. And so Fouque and Vannet [8] provided a practical full key recovery for 784/799 rounds Trivium. Todo et al. [19] proposed a key-recovery attack on 832-round Trivium, where i equivalent bit tin be recovered with complexity of effectually $2^{77}$, combined with division property [18]. All of these attacks exploited low degree properties of the ANF of the output chip over Four bits. As though the degree is non depression, i.e., the degree is equal to the number of variables, there is a possibility to construct distinguishers if there are missing (Four) terms. In [iii, five], Dinur and Shamir exploited the density of Four terms, combined with nullification technique, and broke the total-round Grain128. Based on nullification technique [3, 5], degree evaluation and IV representation techniques were proposed and the missing IV terms can be obtained with probability 1 [9]. The degree upper premises of Trivium-like ciphers were obtained [16] using the degree evaluation techniques. And then a fundamental-recovery attack on 835-circular Trivium was proposed in [17] using correlation cube attack with a complication of $ii^{75}$. Though the cube attack and cube tester tools can be applied to obtain the low-caste information, it is restricted by the computing power. Information technology is hard to execute cube tester programs of dimension more than 50 on a pocket-sized cluster of cores.

In this newspaper, we focus on the cryptanalysis on round-reduced Trivium. We first propose a novel observation of the Boolean polynomial and invent a new nullification technique for reducing the output Boolean polynomial. After nullification, nosotros determine the degree upper bound of the reduced polynomial, which can serve equally the distinguishers. In this process, large quantities of state terms arise to be candy. We present a serial of techniques to help discard monomials, including caste evaluation and degree reduction techniques. Based on these reduction techniques for boolean polynomials, we advise the kickoff key-recovery attack on 855-round Trivium with time complexity $ii^{77}$. We summarize the related results in Table 1.

Table 1. Some related key-recovery results for reduced round Trivium.

Full size table

The residual of the paper is organised as follows. In Sect. 2, some basic related preliminaries will be shown. The basic techniques used in this newspaper and the assault framework will be introduced in Sect. 3. Based on the Boolean polynomial reduction techniques and 4 representation, a key recovery attack on 855-round Trivium is proposed in Sect. 4, combined with a new nullification technique. Finally, Sect. v summarizes the newspaper.

ii Preliminaries

In this section, some bones notations used in this paper are introduced in the following subsections.

2.1 Notations

ii.2 Brief Description of Trivium

Trivium tin can be described past a 288-flake nonlinear feedback shift register $s_{i}$ ($i\le i\le 288$). During the initialization phase, $s_{1}$ to $s_{fourscore}$ are set to 80 key bits, $s_{94}$ to $s_{173}$ are set with 80 IV bits, $s_{286}$, $s_{287}$, $s_{288}$ are fix to 1s and the other country bits are prepare to zeros, i.eastward.,

$(s_1,s_2,\ldots ,s_{93})\leftarrow (K_0,\ldots ,K_{79},0,\ldots ,0)$

$(s_{94},s_{95},\ldots ,s_{177})\leftarrow (IV_0,\ldots ,IV_{79},0,\ldots ,0)$

$(s_{178},s_{179},\ldots ,s_{288})\leftarrow (0,\ldots ,0,one,1,1).$

And then the NFSR is updated for 1152 rounds with the following updating function, i.east.,

$\mathbf {for}$ $i\leftarrow 1:4\cdot 288$ $\mathbf {do}$

$t_{1}\leftarrow s_{66}+s_{91}\cdot s_{92}+s_{93}+s_{171}$

$t_{2}\leftarrow s_{162}+s_{175}\cdot s_{176}+s_{177}+s_{264}$

$t_{3}\leftarrow s_{243}+s_{286}\cdot s_{287}+s_{288}+s_{69}$

$(s_{1},s_{two},\ldots ,s_{93})\leftarrow (t_3,s_{1},\ldots ,s_{92})$

$(s_{94},s_{95},\ldots ,s_{177})\leftarrow (t_1,s_{94},\ldots ,s_{176})$

$(s_{178},s_{179},\ldots ,s_{288})\leftarrow (t_2,s_{178},\ldots ,s_{287})$

$\mathbf {end~for}$

Subsequently the initialization, the output bits $o_{i}$ can be generated past the following functions.

$\mathbf {for}$ $i\leftarrow 1:N$ $\mathbf {do}$

$t_{ane}\leftarrow s_{66}+s_{91}\cdot s_{92}+s_{93}+s_{171}$

$t_{2}\leftarrow s_{162}+s_{175}\cdot s_{176}+s_{177}+s_{264}$

$t_{3}\leftarrow s_{243}+s_{286}\cdot s_{287}+s_{288}+s_{69}$

$o_{i}\leftarrow s_{66}+s_{93}+s_{162}+s_{177}+s_{243}+s_{288}$

$(s_{i},s_{2},\ldots ,s_{93})\leftarrow (t_3,s_{1},\ldots ,s_{92})$

$(s_{94},s_{95},\ldots ,s_{177})\leftarrow (t_1,s_{94},\ldots ,s_{176})$

$(s_{178},s_{179},\ldots ,s_{288})\leftarrow (t_2,s_{178},\ldots ,s_{287})$

$\mathbf {finish~for}$

So the message can be encrypted past sectional-or with $o_{i}$. To outline our technique more conveniently, nosotros draw Trivium using the post-obit iterative expression. We use $s_{w}^{r}$ ($0\le due west\le two$) shown in Eq. one to illustrate r-round ($1\le r\le 1152$) $s_{i}$, $s_{94}$ and $s_{178}$ separately. Let $z_{r}$ denote the output flake afterwards r rounds of initialization. And so the initialization procedure can be illustrated past the following formula

$$\begin{aligned} \begin{array}{ll} s_{0}^{r}&{}=s_{2}^{r-66}+s_{2}^{r-109}s_{ii}^{r-110}+s_{2}^{r-111}+s_{0}^{r-69},\\ s_{1}^{r}&{}=s_{0}^{r-66}+s_{0}^{r-91}s_{0}^{r-92}+s_{0}^{r-93}+s_{1}^{r-78},\\ s_{2}^{r}&{}=s_{1}^{r-69}+s_{1}^{r-82}s_{1}^{r-83}+s_{1}^{r-84}+s_{2}^{r-87}. \stop{assortment} \terminate{aligned}$$

(1)

The $s_{due west}^{r}$ ($0\le w\le 2$) is denoted as internal state scrap in this paper. The multiplication of state $.25 $\displaystyle {\prod _{i\in I,j\in J}s_{i}^{j}}$ is denoted as a land term. The output can be described using the state terms equally $z_{r}=s_{0}^{r-65}+s_{0}^{r-92}+s_{1}^{r-68}+s_{1}^{r-83}+s_{ii}^{r-65}+s_{2}^{r-110}$.

2.3 Representation of Boolean Functions for Stream Ciphers

Supposing that there are m IV bits, i.e., $v_{0},v_{1},\ldots ,v_{m-1}$ and northward key bits, i.e., $k_{0},k_{1},\ldots ,k_{n-1}$, the Algebraic Normal Form (ANF) of the internal state bit or output fleck south could be written equally the following mode:

$$\begin{aligned} due south=\sum _{I,J}\prod _{i\in I}v_{i}\prod _{j\in J}k_{j}, \end{aligned}$$

(2)

where the sum performance is over field $\mathbb {F}_2$. The ${\prod _{i\in I}v_{i}\prod _{j\in J}k_{j}}$ is also denoted as a country term of due south and $\prod _{i\in I}v_{i}$ is denoted as its corresponding IV term. Permit IV term $t_{I}=\prod _{i\in I}v_{i}$ exist the multiplication of $v_{i}$ whose indices are inside I, the ANF of southward can be rewritten as

$$\brainstorm{aligned} s=\sum _{I}t_{I}g_{I}(one thousand), \finish{aligned}$$

(iii)

where $g_{I}(k)$ is the sum of the respective coefficient function of terms whose corresponding IV term is $t_{I}$. The |I| is denoted as the degree of Iv term $t_{I}$, $\deg (t_{I})$. The degree of s is $\deg (s)=\texttt {max}_I\{\deg {(t_I)}\}$.

ii.4 Cube Attack and Cube Tester

Cube attack [4] is introduced by Dinur and Shamir at EUROCRYPT 2009. This method is besides known as high-club differential attack introduced by Lai [fifteen] in 1994. It assumes the output chip of a cipher is a d-degree polynomial $f(k_0...,k_{north-1},v_0...,v_{m-1})$ over GF(2). The polynomial can be written as a sum of two polynomials:

$$f(k_0...,k_{northward-1},v_0...,v_{one thousand-1})=t_I\cdot P+Q_{t_I}(k_0...,k_{n-1},v_0...,v_{one thousand-i})$$

$t_I$ is called maxterm and is a product of certain public variables, for instance $(v_0,...,v_{south-1}),1\le south \le m$, which is called a cube $C_{t_I}$; P is chosen superpoly; $Q_{t_I}(k_0...,k_{n-i},v_0...,v_{m-one})$ is the remainder polynomial and none of its terms is divisible by ${t_I}$. The major idea of the cube attack is that the sum of f over all values of the cube $C_{t_I}$ (cube sum) is:

$$\sum _{x'=(v_0,...,v_{s-1})\in C_{t_I}}f(k_0,...,k_{north-one},x',...v_{m-1}) = P$$

whose degree is at most d-s, where the cube $C_{t_I}$ contains all binary vectors of length s and the other public variables are fixed to constants. In cube attack, P is a linear role over fundamental bits. The primal is recovered by solving a organization of linear equations derived by different cubes $C_{t_I}$.

Dynamic cube attack [v] is besides introduced by Dinur and Shamir in FSE 2011. The basic idea is to notice dynamic variables, which depend on some of the public cube variables and some private variables (the fundamental $.25), to nullify the complex role $P = P_1 \cdot P_2 + P_3$, where the degree of $P_{three}$ is relatively lower than the degree of P and $P_{i} \cdot P_{2}$ is a circuitous function. Then guess the involved key $.25 and compute the dynamic cube variables to brand $P_1$ to be nix and the role is simplified profoundly. The right guess of cardinal bits will lead the cube sum to be zilch otherwise the cube sums will be random generally.

Cube testers [one] are used to discover not-random properties. Suppose in Eq. 3, an Iv term ${t_I}$ does non exist in the ANF of s, e.m. the coefficient $g_{I}(k)=0$. Hence, the cube sum over cube $C_{t_I}$ is definitely zero for unlike key guessing. However, if the IV term ${t_I}$ exists, the value of cube sum $g_{I}(m)$ is dependent on the key guessing. This property was practical to break total-circular Grain128 [5, 9].

3 Basic Ideas

3.1 New Observation of Boolean Polynomial Reduction

In this paper, we propose a new nullification technique based on a lemma as follows.

Lemma 1

Suppose z is the output polynomial of a cipher, and

$$\begin{aligned} z=P_{1}P_{ii}+P_{3}. \cease{aligned}$$

(four)

Then the polynomial can be reduced to a simpler ane $(1+P_{1})z=(ane+P_{1})P_{3}$ by multiplying $1+P_{1}$ in both sides of Eq. (4) if $\deg (P_{1}P_{ii})>\deg ((1+P_{1})P_{3})$.

Lemma one can be verified by $(P_1+1)z=(P_1+1)P_{1}P_2+(P_1+1)P_3=(P_1+1)P_3$. In our cryptanalysis of Trivium, $P_{1}$ is a simple polynomial over several IV bits and key $.25, while $P_{ii}$ is much more complex than $P_{3}$. In our nullification technique, nosotros multiply $P_{one}+1$ in both sides of Eq. (4) to nullify the most complex polynomial $P_2$ without changing $P_3$. The event $(i+P_{1})z=(1+P_{1})P_{3}$ could exist analyzed past considering $P_{3}$ and $ane+P_{1}$ independently, and so multiply them together to become $(1+P_{ane})z$.

3.2 Outline of Our Attack

Based on the novel ascertainment in Sect. iii.1, our attack includes ii phases, which are the preprocessing phase and on-line attack phase.

In the preprocessing phase,

i.
We use the new nullification technique by determining $P_{1}$, and then multiply $ane+P_{1}$ in both sides of Eq. iv and obtain the reduced polynomial $(1+P_{1})P_{3}$.
2.
We study the polynomial $(1+P_{1})P_{3}$ and prove its upper bound degree to be d mathematically, and then cubes of dimension d + 1 pb to distinguishers.

In the on-line phase, nosotros guess the partial fundamental bits in $P_{1}$, and compute the cube sums of $(P_1+1)z$ over ($d+1$)-degree Iv terms:

i
For the correct primal guessing, $(P_1+1)z=(P_1+ane)P_3$. Thus the cube sums must be zero.
ii
For the wrong central guessing, the equation becomes $ (P'_1+1)z=(P'_1+one)P_{1}P_2+(P'_1+1)P_3$, which is more complex and dominated past $P_2$, thus the cube sums are not always aught.

We focus on constructing the distinguishers in the preprocessing phase and it costs near calculating sources.

3.3 Amalgam Distinguishers

Afterward obtaining the reduced polynomial $(1+P_{1})P_{iii}$, our major piece of work is to study this polynomial and derive distinguishers. In our analysis, we demonstrate that the degree of the reduced polynomial is strictly lower than lxx. Equally the caste is so high, such a consequence was hard to reach in previous works. So nosotros introduce various details of reducing polynomials in an iterative process.

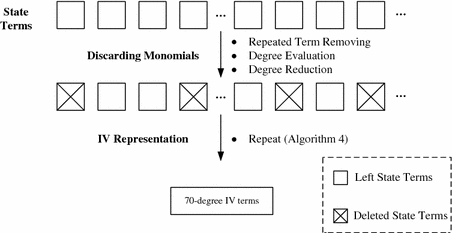
Nosotros innovate several techniques to discard monomials in advance during the iterative computation of the ANF representation of the output bit $(1+P_{1})P_{three}$. Suppose we are proving the upper bound caste of $(i+P_{1})P_{iii}$'s ANF to be d, then the following techniques are used to reduce the Boolean polynomial of $(1+P_{one})P_{three}$ by discarding monomials in advance. The whole process could be divided into the following three steps shown in Fig. 1.

Step 1. Nosotros compute forward to express the ANF of some internal state $.25 over IV $.25 and cardinal bits. In Trivium, the internal country bits $s_{i}^{j}$ ($0\le i\le 2$, $0\le j\le 340$) are computed in a PC.
Stride ii. During the iterative computation of the ANF representation of $(1+P_{1})P_{three}$ in the backward direction (decryption), we introduce the fast discarding monomial technique in Sect. 3.4, which includes the following two algorithms:
- Showtime, nosotros propose the caste evaluation algorithm to obtain the caste bounds of internal state bits. As the monomials of $(1+P_{i})P_{3}$'s ANF is a product of these internal country bits, the degree of a monomial is bounded past the sum of the degrees of the multiplied internal state bits, which is regarded equally the degree estimation of the monomial. If the estimated degrees of monomials are lower than d, they are discarded directly.
- Second, we exploit the iterative structure of Trivium, and find that the $(1+P_{1})P_{3}$'s ANF contains many products of consecutive internal state bits. Thus, we pre-compute the degree reduction southward of those products, which is $d_{t}=\sum _{i}\deg (x_{i})-\deg (\prod _{i}x_{i})$, where $x_{i}$ is an internal state bit. Thus, the caste of a monomial is upper bounded by the deviation value betwixt the sum of the multiplied internal state bits and the respective caste reduction $d_{t}$. If information technology is smaller than d, the monomial is discarded.
Step 3. For the left monomials of $(1+P_{1})P_{3}$'s ANF, nosotros innovate IV representation technique in Sect. 3.5 to determine the upper spring degree of $(1+P_{1})P_{3}$ or find the d-caste missing product of certain IV bits (missing IV term). In IV representation technique, the symbolic key bits in the internal land $.25 are removed and but 4 bits are left. Combining with repeated IV term removing algorithm, nosotros can simplify monomials of $(1+P_{one})P_{3}$'s ANF without losing the missing IV term information. If nosotros detect an 4 term is non in the Iv representation of $(1+P_{i})P_{3}$, we tin can conclude that it is also not in $(1+P_{1})P_{3}$.

iii.4 Fast Discarding Monomial Techniques

In Pace 2 of Fig. 1, during the iterative computation of the ANF representation of $(ane+P_{1})P_{3}$ in the backward direction (decryption), there arise more and more than state terms. Nosotros will give several techniques to simplify the polynomial past discarding monomials in advance. In this Footstep, repeated state terms arise according to the Trivium encryption scheme. The repeated land terms are removed using Algorithm i. The complication of Algorithm one is O(n), supposing there are n state terms.

Degree evaluation technique. As we are proving the degree of the Boolean polynomial $(1+P_{1})P_{3}$ to exist d, thus many monomials with lower caste produced during the iterative ciphering backward (decryption) in Step 3 are deleted without consideration (we do not need to continue the iterative computation over those monomials). We estimate those monomials using degree data of the internal state bits in lower rounds. This section presents a caste evaluation algorithm for the internal country $.25. For example, we are going to estimate the degree of $b_{i}=b_{i-3}+b_{i-1}b_{i-2}$.

$$\begin{aligned} \begin{assortment}{ll} \deg (b_{i}) &{} =\deg (b_{i-3}+b_{i-1}b_{i-two})\\ &{}=\texttt {max}\{\deg (b_{i-iii}), \deg (b_{i-1}b_{i-two})\}\\ &{}\le \texttt {max}\{\deg (b_{i-3}), \deg (b_{i-i})+\deg (b_{i-two})\} \end{assortment} \finish{aligned}$$

(v)

If we go on to decompose $b_{i}$, we find

$$\begin{aligned} \begin{array}{ll} b_{i-1}b_{i-2}&{}=(b_{i-4}+b_{i-2}b_{i-3})(b_{i-5}+b_{i-iii}b_{i-four})\\ &{}=b_{i-four}b_{i-5}+b_{i-3}b_{i-4}+b_{i-two}b_{i-3}b_{i-5}+b_{i-two}b_{i-3}b_{i-4}, \terminate{array} \finish{aligned}$$

(half-dozen)

If $\deg (b_{i-1})=\deg (b_{i-2}b_{i-3})$ and $\deg (b_{i-2})=\deg (b_{i-three}b_{i-4})$, so in Eq. (five), $\deg (b_{i-1})+\deg (b_{i-2})$ may add $\deg (b_{i-three})$ twice. So in social club to obtain a more accurate degree estimation, nosotros are willing to decompose $b_i$ for several rounds backwards.

For Trivium, the ANFs of $s_{i}^{j}$ ($0\le i\le two$, $0\le j\le 340$) are exactly obtained in a PC and their verbal degrees can be obtained. For example, in the cryptanalysis of 855-round Trivium, nosotros compute ANF of $s_{i}^{j}$ ($0\le i\le ii$, $0\le j\le 340$) over 75 gratuitous IV variables^{Footnote one}, the degrees are shown in Tabular array 2. To estimate the degree of $s_{i}^{r}$ for $r>340$, we decompose $s_{i}^{r}$ until the state terms are the product of internal state $.25 $s_{i}^{j}$ for $j < end= \lfloor \frac{r}{32}\rfloor \times 32-128$ considering the efficiency tradeoff of the ciphering.

Table ii. Degree $\deg (s_i^j)$ of $s_{i}^{j}$ for $0\le i\le 2$, $0\le j\le 340$

Full size table

For example, we guess the degree upper bound of $s_{i}^{341}$, where $ terminate=\lfloor \frac{r}{32}\rfloor \times 32-128=192$. Nosotros first express $s_{i}^{341}$ using state $.25 in less rounds, and discard the state terms of degree lower than d.

Step 1. First, we limited $s_{two}^{341}=s_{1}^{272}+s_{one}^{259}s_{1}^{258}+s_{1}^{257}+s_{2}^{254}$ according to Eq. (1).
Step two. According to Table two highlighted in cherry, let $d=\texttt {max}\{\deg (s_{1}^{272}),$ $\deg (s_{i}^{259})+\deg (s_{1}^{258}),\deg (s_{ane}^{257}), \deg (s_{2}^{254}\} = \texttt {max}\{5,5+v,5,5\}=10$.
Stride 3. Discarding the state terms of degree lower than ten, we go $s_{ii}^{341*}=s_{1}^{259}s_{1}^{258}$. Iteratively compute $s_{two}^{341*}$ and discard state terms with degree lower than x, at that place is no country term surviving. Nosotros reset $d=d-1$ and repeat the above decomposition and discarding process. Nosotros tin get the result $s_{ii}^{341**}=s_0^{166}s_0^{167}s_0^{193}+s_0^{167}s_0^{168}s_0^{192}+s_0^{166}s_0^{167}s_0^{168}+s_0^{165}s_0^{167}s_0^{168}+s_0^{167}s_0^{168}s_1^{180}+s_0^{166}s_0^{167}s_1^{181}$.
Stride 4. Note that there is still a state flake $s_{ane}^{193}$ in $s_{ii}^{341**}$ that is bigger than end=192. So nosotros continue to iteratively compute and discard state terms with degree lower than 9, and nosotros go:

$$\begin{aligned} \begin{array}{l} s_{2}^{341***}= s_2^{56}s_2^{57}s_2^{83}s_2^{84}s_2^{101}+s_2^{57}s_2^{58}s_2^{83}s_2^{84}s_2^{100}+s_2^{56}s_2^{57}s_2^{58}s_2^{83}s_2^{84}+\\ s_0^{97}s_2^{57}s_2^{58}s_2^{83}s_2^{84}+s_0^{98}s_2^{56}s_2^{57}s_2^{83}s_2^{84}+s_0^{124}s_2^{56}s_2^{57}s_2^{101}+s_0^{124}s_2^{57}s_2^{58}s_2^{100}+\\ s_0^{124}s_2^{56}s_2^{57}s_2^{58}+s_0^{124}s_2^{55}s_2^{57}s_2^{58}+s_2^{55}s_2^{57}s_2^{58}s_2^{83}s_2^{84}+s_0^{97}s_0^{124}s_2^{57}s_2^{58}\\ +s_0^{98}s_0^{124}s_2^{56}s_2^{57}+s_2^{57}s_2^{58}s_2^{82}s_2^{83}s_2^{102}+s_2^{58}s_2^{59}s_2^{82}s_2^{83}s_2^{101}+s_2^{57}s_2^{58}s_2^{59}s_2^{82}s_2^{83}+\\ s_2^{56}s_2^{58}s_2^{59}s_2^{82}s_2^{83}+s_0^{98}s_2^{58}s_2^{59}s_2^{82}s_2^{83}+s_0^{99}s_2^{57}s_2^{58}s_2^{82}s_2^{83}+s_0^{123}s_2^{57}s_2^{58}s_2^{102}+\\ s_0^{123}s_2^{58}s_2^{59}s_2^{101}+s_0^{123}s_2^{57}s_2^{58}s_2^{59}+s_0^{123}s_2^{56}s_2^{58}s_2^{59}+s_0^{98}s_0^{123}s_2^{58}s_2^{59}\\ +s_0^{99}s_0^{123}s_2^{57}s_2^{58}+s_2^{56}s_2^{57}s_2^{58}s_2^{59}s_2^{101}+s_0^{98}s_2^{56}s_2^{57}s_2^{58}s_2^{59}+s_2^{55}s_2^{56}s_2^{57}s_2^{58}s_2^{102}+\\ s_2^{55}s_2^{56}s_2^{58}s_2^{59}s_2^{101}+s_2^{55}s_2^{56}s_2^{57}s_2^{58}s_2^{59}+s_0^{98}s_2^{55}s_2^{56}s_2^{58}s_2^{59}+s_0^{99}s_2^{55}s_2^{56}s_2^{57}s_2^{58}+\\ s_0^{114}s_2^{57}s_2^{58}s_2^{102}+s_0^{114}s_2^{58}s_2^{59}s_2^{101}+s_0^{114}s_2^{57}s_2^{58}s_2^{59}+s_0^{114}s_2^{56}s_2^{58}s_2^{59}+s_0^{89}s_0^{ninety}s_2^{57}s_2^{58}s_2^{100}+\\ s_0^{98}s_0^{114}s_2^{58}s_2^{59}+s_0^{99}s_0^{114}s_2^{57}s_2^{58}+s_0^{115}s_2^{56}s_2^{57}s_2^{101}+s_0^{115}s_2^{57}s_2^{58}s_2^{100}+s_0^{115}s_2^{56}s_2^{57}s_2^{58}+\\ s_0^{115}s_2^{55}s_2^{57}s_2^{58}+s_0^{97}s_0^{115}s_2^{57}s_2^{58}+s_0^{98}s_0^{115}s_2^{56}s_2^{57}+s_0^{89}s_0^{90}s_2^{56}s_2^{57}s_2^{101}+\\ s_0^{89}s_0^{90}s_2^{56}s_2^{57}s_2^{58}+s_0^{89}s_0^{ninety}s_2^{55}s_2^{57}s_2^{58}+s_0^{89}s_0^{ninety}s_0^{97}s_2^{57}s_2^{58}+s_0^{89}s_0^{90}s_0^{98}s_2^{56}s_2^{57}. \end{array} \end{aligned}$$

(7)
Step 5. Here, at that place is no country bit in rounds more than $end=192$, the expression ends and there are still state terms that survive. Then the current degree $d=nine$ is the estimated degree of $s_{two}^{341}$.
Stride half-dozen. Annotation that, if there is no state item in $s_{ii}^{341***}$ surviving, which ways the degree added twice or more shown in Eq. (6) happens to the iterative computation of $s_{2}^{341}$. So the degree must be less than nine. We reset $d=8$ and continue the above steps iii–5 to get a more than accurate degree bound.

We summarise the to a higher place half-dozen steps as Algorithm 2. Nosotros but estimate caste of $s_{i}^{r}$ for $r\le 665$ and listing the results in Tabular array 3.

Tabular array 3. The estimated upper leap caste $\mathcal {DEG}(s_i^j)$ of $s_{i}^{r}$ for $r\le 689$

Full size table

Degree reduction technique. In this part, we formally consider the belongings in Eq. (vi), that $\deg (b_{i-3})$ is added twice. Nosotros call it degree reduction. Define the degree reduction $d_{t}$ as

$$\begin{aligned} d_{t}=\sum _{i\in I}\deg (x_{i})-\deg (\prod _{i\in I}x_{i}), \end{aligned}$$

(8)

where $x_{i}$ is a land scrap.

We pay attention to the degree reduction of the state term ${\prod _{j=l}^{l+t-1}s_{i}^{j}}$ for a specific $i\in [0,2]$. This country term results from the iteration structure of Trivium scheme, whose high degree land terms come from the multiplication of $s_{i}^{j}s_{i}^{j+1}$ shown in Eq. (i). After several rounds of iteration, the high degree state terms are in the form ${\prod _{j=l}^{fifty+t-1}s_{i}^{j}}$. Define the degree reduction $d_{t}=\sum _{j=l}^{l+t-ane}\deg (s_{i}^{j})-\deg (\prod _{j=fifty}^{l+t-1}s_{i}^{j})$.

The caste reduction can help discard state terms of lower caste dramatically, as it can help predict the modify of degree before expression performance^{Footnote two}. We accept the state term $s_{ane}^{340}s_{1}^{341}$ every bit an example to illustrate the procedure to compute the degree reduction $d_t$. Algorithm 2 is commencement used to obtain the degree of state bits as shown in Tables ii and three.

Allow end exist $\lfloor \frac{r}{32}\rfloor \times 32-128=192$, too. The degree bound d is initialized as $d=\mathcal {DEG}(s_{1}^{340})+\mathcal {DEG}(s_{1}^{341})$ and $d_{t}=0$. Express the $s_{i}^{340}s_{i}^{341}$ by one iteration using Eq. (1). Discard the state terms of caste lower than $d-d_{t}=d$, there is no state term surviving. Increase the $d_{t}$ past 1, such that $d_{t}=1$. Limited $s_{1}^{340}s_{one}^{341}$ again and discard the state terms of caste lower than $d-d_{t}=d-1$, the consequence is $s_{0}^{249}s_{0}^{250}s_{one}^{262}+s_{0}^{248}s_{0}^{249}s_{i}^{263}$. Continue to compute iteratively, the remaining country terms are $s_{0}^{170}s_{0}^{171}s_{0}^{180}s_{2}^{140}s_{ii}^{141}+s_{0}^{170}s_{0}^{171}s_{0}^{181}s_{2}^{139}s_{two}^{140}+s_{0}^{171}s_{0}^{172}s_{0}^{179}s_{ii}^{139}s_{2}^{140}+s_{0}^{171}s_{0}^{172}s_{0}^{180}s_{two}^{138}s_{2}^{139}$. In that location is no country bits $s_{i}^{j}$ with j bigger than $end=192$ in all the state terms, hence the expression ends. Degree reduction $d_{t}=1$ is returned. Thus the $\deg (s_{1}^{340}s_{1}^{341})\le \mathcal {DEG}(s_{1}^{340})+\mathcal {DEG}(s_{1}^{341}) - d_t= vii+7-ane=13$. The degree reduction algorithm is shown in Algorithm 3

3.5 Iv Representation Techniques

In the cryptanalysis of stream ciphers, the output is a boolean function over primal and 4 bits. But obtaining the exact expression is hard, thus we propose IV representation technique to reduce the computation complexity for obtaining the degree information.

Definition 1

(4 representation) Given a state bit $s=\sum _{I,J}\prod _{i\in I}v_{i}\prod _{j\in J}k_{j}$, the 4 representation of south is $s_{Iv}=\sum _{I}\prod _{i\in I}v_{i}$.

For case, if a boolean polynomial is $s=v_{0}k_{one}+v_{0}k_{0}k_{2}+v_{1}k_{1}k_{2}+v_{0}v_{i}k_{two}$, and so its corresponding IV representation is $s_{4}=v_{0}+v_{0}+v_{i}+v_{0}v_{1}$.

Iv representation with repeated Iv terms Removing Algorithm. Due to neglection of key bits, there are lots of repeated Iv terms. Here we give an algorithm to remove the repeated IV terms of $s_{4}$. The details of the algorithm are shown in Algorithm 4. This algorithm is based on a Hash function. First, an empty hash fix is initialized. For each IV term $T_{i}$, compute the hash value as $H(T_{i})$ (Line iii), and then determine if $T_{i}$ is already in H. If not, and so insert $T_{i}$ into H (Lines four–5). Applying Algorithm 4 to the above instance, the issue is $v_{0}+v_{ane}+v_{0}v_{ane}$. Note that this algorithm is slightly different from Algorithm one. If we utilise Algorithm 1 to $s_{IV}$, the upshot is $v_{i}+v_{0}v_{one}$.

In the iterative computation process of the output scrap of Trivium, it should be noted that if an IV term exists in s, it must likewise be in $s_{Iv}$, but not the opposite. For case, $x_1 = v_0(k_1k_2+k_0k_2)+v_1 + v_0v_1k_2$, $x_2 = v_2k_0k_1 + v_1v_2k_1$ and $s=x_1x_2$. Nosotros use the Iv representations of $x_1$ and $x_2$ to approximate the IV representation of s. Thus, $x_{1IV}=v_0+v_1+v_0v_1$, $x_{2IV}=v_2+v_1v_2$, and $s_{IV}=x_{1IV}x_{2IV}=v_0v_2+v_1v_2+v_0v_1v_2$. All the same, $southward=x_1x_2=v_1v_2(k_0k_1+k_1)$. So if we find an Four term is not in $s_{IV}$, we tin can conclude that information technology is not in s either . We utilise this to determine the caste upper bound of the output ANF of Trivium.

After using Iv representation combined with Algorithm 4, all the existent Iv terms are left past ignoring their repetition. With collision-resistent hash function H, the fourth dimension complexity of Algorithm 4 is O(n) for processing n Iv terms. It needs several minutes to apply Algorithm 4 on 1 billion IV terms on a unmarried core.

four Key Recovery Attack on 855-circular Trivium

In the attack on 855-circular Trivium, all the 80-bit Four are initiated with free variables: $IV_{i}=v_{i}$, $i\in [0,79]$.

The output of 855-round Trivium can be described using the internal country bits:

$$\begin{aligned} z_{855}=s_{0}^{790}+s_{0}^{763}+s_{1}^{787}+s_{1}^{772}+s_{2}^{790}+s_{2}^{745}. \end{aligned}$$

(9)

As a first step of the attack on 855-round Trivium, we need to determine $P_{i}$.

4.1 Determining the Nullification Scheme for the Output Polynomial of 855-round Trivium

For 855-round Trivium, the degree of output chip z is very high, as shown in [19]. So it is non easy to find the missing Four terms in the complex $z=P_{1}P_{2}+P_{3}$. Nevertheless, based on the new observation of Boolean polynomial introduced in Sect. three.1. we tin can choose $P_{1}$ to reduce the Boolean polynomial $(ane+P_{1})z=(1+P_{ane})P_{iii}$ such that the degree of $(1+P_{one})P_{3}$ is lower. The lower, the ameliorate. In fact, the lower the degree of a state term, the less loftier caste Four terms it can deduce.

Degrees of country bits are obtained first in society to determine the high degree land terms. The exact Boolean polynomial of $s_{i}^{j}$ for $i\in [0,2]$ and $j\in [0,340]$ can be obtained. The other degree upper bounds can be obtained by executing Algorithm 2.

For a search of $P_1$, we utilise the decomposition of Trivium and preserve the high degree land terms (bigger than a given bound dependent on our computing ability in a PC), where the degree of state terms ways the sum of degrees of each state scrap in the earlier rounds involved. We decompose until all the state bits are within the range of [0, 276]. The key points to determine $P_1$ come up from iii criteria: (1) the frequency of $P_1$ is high; (2) the degree of $P_1$ is depression; (3) the equivalent key guesses in $P_1$ are minimized. We calculate the frequency of state $.25 and find that $s_1^{210}$ occurs in about $\frac{three}{iv}$ of all the preserved high state terms. The degree of $s_1^{210}$ is 5 and can be reduced to 2 afterwards nullifying the 5 IV bits, and there are only 3 equivalent key bits to be guessed. So nosotros cull $P_1= s_1^{210}$.

The output polynomial tin can be rewritten equally

$$\begin{aligned} z=s_{1}^{210}P_{two}+P_{three}, \cease{aligned}$$

(x)

where $P_{2}$ and $P_{iii}$ do not incorporate $s_{one}^{210}$. Polynomial $P_{two}$ is and so complex that it is hard to compute its degree and density information while $P_{3}$ is relatively simple. Here $P_{1}=s_{1}^{210}=v_{59}v_{threescore}v_{61}+v_{59}v_{60}v_{76}$ $+v_{17}v_{59}v_{60}+v_{30}v_{31}v_{59}v_{lx}+v_{32}v_{59}v_{threescore}+v_{59}v_{sixty}v_{62}+v_{59}v_{60}v_{77}+v_{59}v_{threescore}k_{20}$ $+v_{59}v_{61}v_{73}v_{74}+v_{59}v_{73}v_{74}v_{76}+v_{17}v_{59}v_{73}v_{74}+v_{thirty}v_{31}v_{59}v_{73}v_{74}+v_{32}v_{59}v_{73}v_{74}+$ $v_{59}v_{62}v_{73}v_{74}+v_{59}v_{73}v_{74}v_{77}+v_{59}v_{73}v_{74}k_{20}+v_{59}v_{lx}v_{74}v_{75}+v_{59}v_{sixty}v_{75}v_{76}+$ $v_{59}v_{73}v_{74}v_{75}+v_{59}v_{73}v_{74}v_{75}v_{76}+v_{59}v_{61}v_{75}+v_{59}v_{74}v_{75} +v_{17}v_{59}v_{75}+v_{30}v_{31}v_{59}v_{75}+$ $v_{32}v_{59}v_{75}+v_{59}v_{62}v_{75}+v_{59}v_{75}v_{77}+v_{59}v_{75}k_{20}+v_{60}v_{61}v_{72}v_{73}+v_{lx}v_{72}v_{73}v_{76}+$ $v_{17}v_{threescore}v_{72}v_{73}+v_{30}v_{31}v_{sixty}v_{72}v_{73}+v_{32}v_{threescore}v_{72}v_{73}+v_{60}v_{62}v_{72}v_{73}+v_{60}v_{72}v_{73}v_{77}+$ $v_{sixty}v_{72}v_{73}k_{20}+v_{61}v_{72}v_{73}v_{74}+v_{72}v_{73}v_{74}v_{76}+v_{17}v_{72}v_{73} v_{74}+v_{30}v_{31}v_{72}v_{73}v_{74}+$ $v_{32}v_{72}v_{73}v_{74}+v_{62}v_{72}v_{73}v_{74}+v_{72}v_{73}v_{74}v_{77}+v_{72}v_{73}v_{74}k_{20} +v_{60}v_{72}v_{73}v_{74}v_{75}+$ $v_{sixty}v_{72}v_{73}v_{75}v_{76}+v_{72}v_{73}v_{74}v_{75}v_{76}+v_{61}v_{72}v_{73}v_{75}+v_{17}v_{72}v_{73}v_{75}+v_{30}v_{31}v_{72}v_{73}v_{75}+$ $v_{32}v_{72}v_{73}v_{75}+v_{62}v_{72}v_{73}v_{75}+v_{72}v_{73}v_{75}v_{77}+v_{72}v_{73}v_{75}k_{xx} +v_{60}v_{61}v_{74}+v_{threescore}v_{74}v_{76}+$ $v_{17}v_{60}v_{74}+v_{30}v_{31}v_{60}v_{74}+v_{32}v_{60}v_{74}+v_{lx}v_{62}v_{74}+v_{60}v_{74}v_{77}+v_{60}v_{74}k_{20}+$ $v_{17}v_{73}v_{74}+v_{thirty}v_{31}v_{73}v_{74}+v_{32}v_{73}v_{74}+v_{62}v_{73}v_{74}+v_{73}v_{74}v_{77}+v_{73}v_{74}k_{20} +$ $v_{16}v_{lx}v_{61}+v_{16}v_{threescore}v_{74}v_{75}+v_{16}v_{lx}v_{76}+v_{16}v_{61}v_{73}v_{74}+v_{16}v_{73}v_{74}v_{75}+v_{xvi}v_{73}v_{74}v_{76}+$ $v_{sixteen}v_{61}v_{75} +v_{16}v_{74}v_{75}+v_{16}v_{17}+v_{16}v_{30}v_{31}+v_{xvi}v_{32}+v_{xvi}v_{62}+v_{16}v_{77}+v_{16}k_{20}+$ $v_{29}v_{xxx}v_{lx}v_{61}+v_{29}v_{thirty}v_{60}v_{74}v_{75}+v_{29}v_{30}v_{sixty}v_{76}+v_{29}v_{30}v_{61}v_{73}v_{74}+v_{29}v_{xxx}v_{73}v_{74}v_{75}+$ $v_{29}v_{30}v_{73}v_{74}v_{76}+v_{29}v_{30}v_{61}v_{75}+v_{29}v_{30}v_{74}v_{75}+v_{17}v_{29}v_{30}+v_{29}v_{30}v_{31}+v_{29}v_{xxx}v_{32}+$ $v_{29}v_{30}v_{62}+v_{29}v_{30}v_{77}+v_{29}v_{30}k_{xx}+v_{31}v_{threescore}v_{61}+v_{31}v_{60}v_{74}v_{75} +v_{31}v_{threescore}v_{76}+$ $v_{31}v_{61}v_{73}v_{74}+v_{31}v_{73}v_{74}v_{75}+v_{31}v_{73}v_{74}v_{76}+v_{31}v_{61}v_{75}+v_{31}v_{74}v_{75}+v_{17}v_{31}+$ $v_{30}v_{31}+v_{31}v_{62}+v_{31}v_{77}+v_{31}k_{20}+v_{60}v_{61}+v_{61}v_{75}+v_{61}v_{74}v_{75}+v_{17}v_{61}+v_{xxx}v_{31}v_{61}+$ $v_{32}v_{61}+v_{61}k_{xx}+v_{60}v_{74}v_{75}v_{76}+v_{60}v_{76}+v_{73}v_{74}v_{75}v_{76}+v_{17}v_{76}+v_{xxx}v_{31}v_{76}+$ $v_{32}v_{76}+v_{76}v_{77}+v_{76}k_{20}+v_{60}v_{61}k_{nineteen}+v_{60}v_{74}v_{75}k_{19}+v_{60}v_{76}k_{nineteen}+v_{61}v_{73}v_{74}k_{xix}+$ $v_{73}v_{74}v_{75}k_{19}+v_{73}v_{74}v_{76}k_{19}+v_{61}v_{75}k_{nineteen}+v_{74}v_{75}k_{19}+v_{17}k_{19}+v_{30}v_{31}k_{19}+v_{32}k_{19}+$ $v_{62}k_{19}+v_{77}k_{19}+k_{19}k_{20}+v_{34}v_{35}+v_{34}v_{48}v_{49}+v_{34}v_{50}+v_{35}v_{47}v_{48}+v_{47}v_{48}v_{49}+$ $v_{47}v_{48}v_{l}+v_{35}v_{49}+v_{48}v_{49}+k_{57}+v_{69}+v_{4}v_{5}+v_{vi}+v_{36}+v_{51}+v_{sixty}+v_{73}v_{74}+$ $v_{75}+k_{63}+v_{62}v_{74}v_{75}+v_{74}v_{75}v_{77}+v_{75}v_{76}+v_{18}+v_{33}+v_{63}+v_{78}+k_{21}+k_{28}k_{29}+$ $k_{3}+k_{30}+k_{12}+k_{37}k_{38}+k_{39}+v_{24}$.

IV Nullification. The degree of $s_{1}^{210}$ is 5 and the 4 bits involved in $s_{ane}^{210}$ are shown in Table iv.

Tabular array iv. Count of IV $.25 in $s_{1}^{210}$ earlier Iv nullification.

Full size table

In lodge to simplify $s_{1}^{210}$ so that information technology is easier to obtain the degree bound of $(1+s_{1}^{210})P_{3}$, nosotros nullify $v_{74}$, $v_{lx}$, $v_{75}$, $v_{30}$ and $v_{48}$.

Afterwards nullifying the 5 4 $.25, we obtain the simplified boolean function:

$$\begin{aligned} \begin{array}{l} s_{i}^{210}=v_{16}v_{17}+v_{16}v_{32}+v_{sixteen}v_{62}+v_{16}v_{77}+v_{16}k_{20}+v_{17}v_{31}+v_{31}v_{62}+\\ v_{31}v_{77}+v_{31}k_{20}+v_{17}v_{61}+v_{32}v_{61}+v_{61}k_{20}+v_{17}v_{76}+v_{32}v_{76}+v_{76}v_{77}+\\ v_{76}k_{twenty}+v_{17}k_{nineteen}+v_{32}k_{19}+v_{62}k_{19}+v_{77}k_{19}+k_{19}k_{20}+v_{34}v_{35}+v_{34}v_{50}+\\ v_{35}v_{49}+k_{57}+v_{69}+v_{4}v_{v}+v_{6}+v_{36}+v_{51}+k_{63}+v_{18}+v_{33}+v_{63}+\\ v_{78}+k_{21}+ k_{28}k_{29}+k_{three}+k_{30}+k_{12}+k_{37}k_{38}+k_{39}+v_{24}. \end{array} \terminate{aligned}$$

(eleven)

Hither, the degree of $s_{1}^{210}$ is 2 and primal data equivalent to three $.25 in $s_{1}^{210}$ are $k_{nineteen}$, $k_{20}$ and $k_{57}+k_{63}+k_{21}+k_{28}k_{29}+k_{3}+k_{30}+k_{12}+k_{37}k_{38}+k_{39}$. The Iv bits involved in $s_{1}^{210}$ are shown in Tabular array 5.

After determining $P_{one}=s_{i}^{210}$, we multiply $ane+s_{1}^{210}$ in both sides of Eq. (x), then $(ane+s_{1}^{210})z=(1+s_{i}^{210})P_{3}$. Finding the non-randomness in $(1+s_{1}^{210})P_{three}$ will aid us to construct the cube tester of 855-round Trivium. More than specifically, we volition determine the nonexistent Four terms of degree seventy in $(1+s_{1}^{210})P_{3}$. First, we will reduce the polynomial, then Iv presentation technique is applied to decide the nonexistent IV terms. The framework is presented in Fig. two and details are shown in the post-obit Sect. iv.2.

Table v. Frequency of IV $.25 in $s_{i}^{210}$ after IV nullification.

Full size tabular array

iv.2 Determining the Degree Bound of Reduced Polynomial

Nosotros are going to iteratively compute $(1+s_{1}^{210})P_{3}$. In each iteration, many state terms of $(1+s_{i}^{210})P_{3}$ are produced. Based on our computing ability, we can compute the Iv terms of caste effectually 70. In computing the lxx-degree Iv terms, we use a cluster of 600–2400 cores. Since we are finding the 70-caste missing IV terms, land terms with degree less than seventy are removed without consideration, because they exercise not incorporate those 70-caste Iv terms certainly. The removing process could exist divided into 2 steps:

one.
Deleting country terms co-ordinate to degree evaluation;
two.
Deleting country terms according to degree reduction.

Degree evaluation phase. Later nullifying the 5 Four $.25 in Sect. iv.ane, the exact boolean functions and degrees of state bits $s_{i}^{j}$ for $0\le i\le 2$ and $0\le j\le 340$ can be updated. Then we execute Algorithm 2 to obtain the degrees of the other state bits, partially in Tables ii and 3. For case, given a state term $b_1b_2$, we first observe $\mathcal {DEG}(b_1)$ and $\mathcal {DEG}(b_2)$ in Tables 2 and 3, if $\mathcal {DEG}(b_1)+\mathcal {DEG}(b_2)<seventy$, then $\deg (b_1b_2)\le \mathcal {DEG}(b_1)+\mathcal {DEG}(b_2)<70$, delete $b_1b_2$.

Caste reduction stage. In the structure of stream ciphers based on NFSR, degree reduction arises oftentimes due to the iterative construction. We utilise Algorithm 3 to obtain the degree reduction, which is shown in Tables vi, 7 and eight for products of two consecutive state bits $s_i^js_i^{j+1}$ ($t=2$), iii consecutive state $.25 $s_i^js_i^{j+ane}s_i^{j+2}$ ($t=3$) and 4 consecutive state bits $s_i^js_i^{j+ane}s_i^{j+two}s_i^{j+3}$ ($t=4$), respectively. Annotation that we only listing the caste reduction when $j\ge 340$. The degree reduction for $j<340$ is much easier to obtain in a PC.

Table 6. Degree reductions $d_t(s_i^js_i^{j+ane})$ of $s_i^js_i^{j+i}$ with $t=2$

Full size table

In the cryptanalysis of Trivium, the caste reduction may be more than complicated. Farther degree reduction for $t>4$ is hard to exist obtained using PC for loop executing Algorithm iii. Some man-made piece of work should be involved to obtain further degree reduction. The degree reduction can help discard state terms of lower degree dramatically. For example, if the state term $b_{1}b_{ii}$ goes through degree evaluation phase, that means $\mathcal {DEG}(b_1)+\mathcal {DEG}(b_2)\ge 70$, then we check if $\mathcal {DEG}(b_1)+\mathcal {DEG}(b_2)-d_t(b_1b_2)<70$. If yep, $\deg (b_1b_2)<lxx$ and delete it.

For example, the Eq. (9) can be expressed furthermore using state bits: 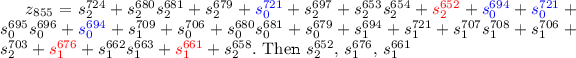, can be discarded because their degree are lower than 68, shown in Table iii highlighted in red, and the total degree of the multiplication of each one with $(1+s_{210})$ is lower than lxx. In addition, the state terms highlighted in blueish can exist discarded past removing the repeated state terms. Furthermore, the output can be expressed using state bits in lower rounds and more state terms can be discarded.

Table 7. Degree reductions $d_t(s_i^js_i^{j+ane}s_i^{j+2})$ of $s_i^js_i^{j+1}s_i^{j+two}$ with $t=3$

Total size tabular array

Table 8. Degree reductions $d_t(s_i^js_i^{j+i}s_i^{j+ii}s_i^{j+3})$ of $s_i^js_i^{j+1}s_i^{j+2}s_i^{j+3}$ with $t=4$

Full size tabular array

After the above 2 steps to reduce $(one+s_{1}^{210})P_{3}$, the degrees of the left state terms are possibly higher or equal to seventy. As the dimension is high, a cube tester over such a big dimension is far beyond our computing power. For the left state terms, we use Four representation for each left state terms and remove the repeated Four terms using Algorithm 4 in order to determine the missing 70-degree IV terms. After the above steps, there is no lxx-degree 4 term in $(1+s_{1}^{210})P_{three}$. And so the degree of $(1+s_{i}^{210})P_{3}$ is strictly lower than 70, which is summarized as the following Lemma 2.

Lemma two

Set the $v_{74}$, $v_{60}$, $v_{75}$, $v_{30}$ and $v_{48}$ to zeros, then the degree of $(1+s_{1}^{210})z_{855}$ is bounded by 70, where $z_{855}$ is the output after 855-circular initializations.

According to Lemma 2, we strictly testify that the degree of the reduced polynomial is lower than lxx, so the sum over any selected cube of dimension 70 is zero, such that the distinguishers can be constructed.

4.3 Online Phase and Complexity Analysis

We beginning guess the three key bits in $s^{210}_{1}$, i.e. $k_{19}$, $k_{20}$ and $k_{57}+k_{63}+k_{21}+k_{28}k_{29}+k_{3}+k_{30}+k_{12}+k_{37}k_{38}+k_{39}$ equally shown in Eq. (eleven), for the right guess the upshot is 0 while for wrong guesses, the result is i with probability $\frac{one}{2}$. If the sum over cubes of dimension 70 is 1, then the cardinal approximate is wrong and dropped (Line 7). After the starting time cube sum, nigh one-half key bits remain, and sum over another cube over again. The remaining guess is the cardinal. The on-line phase is shown in Algorithm 5.

For each guess, we demand to sum over a cube of dimension 70, and so that the complexity is $two^{three}\cdot 2^{seventy}+2^{two}\cdot 2^{70}+2^{1}\cdot 2^{70}\approx 2^{74}$.

After the above process, the bits $k_{19}$, $k_{20}$ and $k_{57}+k_{63}+k_{21}+k_{28}k_{29}+k_{three}+k_{30}+k_{12}+k_{37}k_{38}+k_{39}$ tin can be determined. $k_{19}$ and $k_{20}$ are single primary fundamental bits. Let $c=k_{57}+k_{63}+k_{21}+k_{28}k_{29}+k_{3}+k_{30}+k_{12}+k_{37}k_{38}+k_{39}$ (c is 0 or 1), then information technology can be rewritten as $k_{57}=k_{63}+k_{21}+k_{28}k_{29}+k_{iii}+k_{30}+k_{12}+k_{37}k_{38}+k_{39}+c$. We guess the other 77 primal bits excluding $k_{xix}$, $k_{20}$ and $k_{57}$, the value $k_{57}$ can exist obtained directly. Then the other 77 key bits excluding $k_{xix}$, $k_{xx}$ and $k_{57}$ can be recovered by fauna force. Thus the complexity to recover all the primal $.25 is $2^{77}$.

4.4 Experimental Verification

Nosotros utilise a powerful nullification technique to reduce the output polynomial, and prove the caste bound of the reduced polynomial theoretically and recover key $.25. To brand the attack more articulate, we give an assail instance. We give two attacks on 721-circular Trivium: a distinguishing attack and a key-recovery assault.

Obtain the Degree Upper Jump of Output of 721-round Trivium. Initial $IV_{i}=v_{i}$ with $i\in [0,79]$. In the example attack on 721-round Trivium, nosotros only use twoscore liberty variables, i.e. fix $v_{ii\cdot j+ane}=0$ for $j\in [0,39]$ and the other 40 IV bits are freedom variables.

The exact boolean functions of the start 340 state bits $s_{i}^{j}$ for $i\in [0,ii]$ and $j\in [0,340]$ tin can be obtained directly on PC. Hence, the degrees of them can be obtained straight. Degrees upper bounds of other land bits tin can be evaluated using Algorithm 2 and are shown in Tabular array 9. Note that in Table 9, the estimated degrees of some state bits are larger than xl, e.g. $\mathcal {DEG}(s_2^{665})=41$, which is because the accurateness of Algorithm two decreases for state $.25 with large rounds. Thus we only utilise this algorithm to $s_i^j$ for $j\le 665$.

Tabular array nine. Degree upper bounds $\mathcal {DEG}(s_i^j)$ of the state $.25 $s_i^j$ for $j\le 665$

Full size table

The output of 721-circular Trivium is $z_{721}=s_{0}^{656}+s_{0}^{629}+s_{ane}^{653}+s_{one}^{638}+s_{2}^{656}+s_{2}^{611}$. According to Table ix, the 6 state terms ($.25) highlighted in red are of degree lower than twoscore, so the degree of $z_{721}$ is lower than 40, which can serve as distinguishers. This result can be obtained easily by rough calculating.

Next, we give a more authentic jump of $z_{721}$. In the following, we volition determine whether $z_{721}$'s caste is bigger than 37. The 6 state $.25 are expressed using state bits in lower rounds once again and substituted into $z_{721}$, which is called the substitution or expression process in [9]. Then $z_{721}=s_{2}^{590}+s_{two}^{546}s_{two}^{547}+$ $s_{2}^{545}+s_{0}^{587}+s_{2}^{563}+s_{2}^{519}s_{2}^{520}+s_{ii}^{518}+s_{0}^{560}+s_{0}^{587}+s_{0}^{561}s_{0}^{562}+s_{0}^{560}+s_{i}^{575}+s_{0}^{572}+$ $s_{0}^{546}s_{0}^{547}+s_{0}^{545}+s_{one}^{560}+s_{i}^{587}+s_{one}^{573}s_{ane}^{574}+s_{one}^{572}+s_{ii}^{569}+s_{ane}^{542}+s_{1}^{528}s_{1}^{529}+s_{1}^{527}+s_{2}^{524}$. Co-ordinate to degree upper bounds Tabular array ix, $\deg (s_{2}^{590})=27<37$ highlighted in blue, and so $s_{2}^{590}$ is removed. And so $\deg (s_{ii}^{546}s_{2}^{547})\le \mathcal {DEG}(s_{ii}^{546})+\mathcal {DEG}(s_{ii}^{547})=20+21=41$ and $41\ge 37$, and then the caste of $s_{two}^{546}s_{2}^{547}$ is peradventure bigger than 36 and left. Afterward discarding all the state terms whose degrees are lower than 36, $z_{721}|_{\deg >36}=s_{ii}^{546}s_{two}^{547}+s_{ane}^{573}s_{i}^{574}$. Continue exchange and expression procedure for $z_{721}|_{\deg >36}$ and finally, in that location remain no state terms with degree bigger than 36, then that the degree bound of $z_{721}$ is 36. The details of the above pace are shown in Appendix A.

A Key-Recovery Assail on 721-round Trivium. Like to the IV setting above for distinguishing 721-round Trivium, we fix $v_{2\cdot j+one}=0$ for $j\in [0,39]$ and the other 40 IV $.25 are freedom variables.

Co-ordinate to our attack outline introduced in Sect. iii.2, we need to make up one's mind the nullification scheme offset. Nosotros express the output of 721-circular Trivium iteratively and calculate the frequency of state bits in the polynomial. Then we choose $s_{1}^{290}$ as $P_{ane}$, the output can be rewritten as $z_{721}=s_{1}^{290}P_{2}+P_{3}$. Multiply $1+s_{1}^{290}$ with $z_{721}$ such that the result is $(1+s_{1}^{290})z_{721}=(1+s_{1}^{290})P_{three}$. We study the reduced polynomial $(1+s_{1}^{290})P_{3}$. In gild to subtract the number of key bits in $s_{one}^{290}$, we choose to nullify $v_{58}$, $v_{64}$ and $v_{72}$, so that there are 37 freedom variables. Ready the degree spring to 32, we express $(1+s_{ane}^{290})P_{iii}$ using internal state bits furthermore and discard land terms whose degree are lower than $32+d_{t}$, where $d_{t}$ is the corresponding degree reduction. We apply IV presentation, combined with Algorithm 4 in order to obtain the IV terms of degree higher than 32. Finally, there is no IV term. Hence, nosotros testify that the degree of $(1+s_{i}^{290})z_{721}$ is lower than 32. Then the sum of $(1+s_{1}^{290})z_{721}$ over any selected cube of dimension 32 is nil. This procedure can be executed in an 60 minutes in a PC.

Guess the key bit involved in $s_{1}^{290}$. For right guess, sum over a cube of dimension 32 is zero while for incorrect guesses, the event is one with probability $\frac{one}{2}$. The primal bits involved in $s_{1}^{290}$ are shown in Tabular array ten. After 19 summations over cubes of dimension 32, the xix key bits can be recovered. The complexity is well-nigh $two\times 2^{xix}\times two^{32}=ii^{52}$. The other key bits tin be recovered using creature strength with a complexity of $2^{61}$. Hence, the total complexity of recovering all key $.25 of 721-round Trivium is $ii^{61}$.

Table 10. The key $.25 involved in $s_{ane}^{290}$.

Total size table

v Conclusions

In this paper, we suggest the Boolean polynomial reduction techniques and IV representation, which can exist applicative to cryptanalysis of stream ciphers based on NFSRs. These techniques can help obtain more accurate degree premises. We use these techniques to the cryptanalysis of reduced circular Trivium. For recovering the key $.25 of Trivium, we propose a new nullification technique. Combined with the distinguishers, we propose a central-recovery assail on 855 round Trivium, where 3 equivalent key bits tin can be recovered with complexity of $2^{74}$. The other key bits tin can exist recovered by brute force with a complication of $2^{77}$.

Furthermore, our flexible methods can be practical to attack more circular of Trivium by adjustment of $P_{1}$, which is our future work. In addition, the degree evaluation and degree reduction techniques tin be applicable to other encryption primitives such as Grain family.

Notes

i.
The other 5 IV bits are fixed as nil and their positions are given in Sect. 4.1.
two.
The details are given in Sect. 4.2.

References

Aumasson, J.-P., Dinur, I., Meier, W., Shamir, A.: Cube testers and key recovery attacks on reduced-round MD6 and Trivium. In: Dunkelman, O. (ed.) FSE 2009. LNCS, vol. 5665, pp. one–22. Springer, Heidelberg (2009). https://doi.org/ten.1007/978-3-642-03317-9_1

CrossRef Google Scholar
De Cannière, C., Preneel, B.: Trivium. In: Robshaw, Yard., Billet, O. (eds.) New Stream Cipher Designs. LNCS, vol. 4986, pp. 244–266. Springer, Heidelberg (2008). https://doi.org/ten.1007/978-iii-540-68351-3_18

CrossRef Google Scholar
Dinur, I., Güneysu, T., Paar, C., Shamir, A., Zimmermann, R.: An experimentally verified assail on full grain-128 using dedicated reconfigurable hardware. In: Lee, D.H., Wang, X. (eds.) ASIACRYPT 2011. LNCS, vol. 7073, pp. 327–343. Springer, Heidelberg (2011). https://doi.org/x.1007/978-3-642-25385-0_18

CrossRef Google Scholar
Dinur, I., Shamir, A.: Cube attacks on tweakable black box polynomials. In: Joux, A. (ed.) EUROCRYPT 2009. LNCS, vol. 5479, pp. 278–299. Springer, Heidelberg (2009). https://doi.org/ten.1007/978-3-642-01001-9_16

CrossRef Google Scholar
Dinur, I., Shamir, A.: Breaking grain-128 with dynamic cube attacks. In: Joux, A. (ed.) FSE 2011. LNCS, vol. 6733, pp. 167–187. Springer, Heidelberg (2011). https://doi.org/10.1007/978-three-642-21702-9_10

CrossRef Google Scholar
Englund, H., Johansson, T., Sönmez Turan, One thousand.: A framework for chosen IV statistical analysis of stream ciphers. In: Srinathan, K., Rangan, C.P., Yung, M. (eds.) INDOCRYPT 2007. LNCS, vol. 4859, pp. 268–281. Springer, Heidelberg (2007). https://doi.org/10.1007/978-3-540-77026-8_20

CrossRef Google Scholar
Fischer, S., Khazaei, South., Meier, W.: Chosen IV statistical analysis for key recovery attacks on stream ciphers. In: Vaudenay, S. (ed.) AFRICACRYPT 2008. LNCS, vol. 5023, pp. 236–245. Springer, Heidelberg (2008). https://doi.org/ten.1007/978-3-540-68164-9_16

CrossRef Google Scholar
Fouque, P.-A., Vannet, T.: Improving key recovery to 784 and 799 rounds of Trivium using optimized cube attacks. In: Moriai, S. (ed.) FSE 2013. LNCS, vol. 8424, pp. 502–517. Springer, Heidelberg (2014). https://doi.org/ten.1007/978-3-662-43933-3_26

CrossRef Google Scholar
Fu, 10., Wang, X., Chen, J.: Determining the nonexistent terms of not-linear multivariate polynomials: how to pause grain-128 more efficiently. IACR Cryptology ePrint Annal 2017, 412 (2017). http://eprint.iacr.org/2017/412
International Arrangement for Standardization (ISO): ISO/IEC 29192–three:2012, Information technology - Security techniques - Lightweight cryptography - Office 3: Stream ciphers (2012)

Google Scholar
Knellwolf, S., Meier, Due west., Naya-Plasencia, M.: Provisional differential cryptanalysis of NLFSR-based cryptosystems. In: Abe, M. (ed.) ASIACRYPT 2010. LNCS, vol. 6477, pp. 130–145. Springer, Heidelberg (2010). https://doi.org/ten.1007/978-3-642-17373-8_8

CrossRef Google Scholar
Knellwolf, Due south., Meier, W., Naya-Plasencia, Grand.: Conditional differential cryptanalysis of Trivium and KATAN. In: Miri, A., Vaudenay, South. (eds.) SAC 2011. LNCS, vol. 7118, pp. 200–212. Springer, Heidelberg (2012). https://doi.org/x.1007/978-3-642-28496-0_12

CrossRef Google Scholar
Knudsen, 50.R.: Truncated and higher order differentials. In: Preneel, B. (ed.) FSE 1994. LNCS, vol. 1008, pp. 196–211. Springer, Heidelberg (1995). https://doi.org/x.1007/3-540-60590-8_16

CrossRef Google Scholar
Knudsen, L., Wagner, D.: Integral cryptanalysis. In: Daemen, J., Rijmen, V. (eds.) FSE 2002. LNCS, vol. 2365, pp. 112–127. Springer, Heidelberg (2002). https://doi.org/10.1007/3-540-45661-9_9

CrossRef Google Scholar
Lai, 10.: College order derivatives and differential cryptanalysis. In: Blahut, R.Eastward., Costello, D.J., Maurer, U., Mittelholzer, T. (eds.) Communications and Cryptography, pp. 227–233. Springer, Boston (1994). https://doi.org/10.1007/978-1-4615-2694-0_23

CrossRef Google Scholar
Liu, K.: Degree evaluation of NFSR-based cryptosystems. In: Katz, J., Shacham, H. (eds.) CRYPTO 2017. LNCS, vol. 10403, pp. 227–249. Springer, Cham (2017). https://doi.org/x.1007/978-iii-319-63697-9_8

CrossRef Google Scholar
Liu, One thousand., Yang, J., Wang, W., Lin, D.: Correlation cube attacks: from weak-central distinguisher to key recovery. Cryptology ePrint Annal, Study 2018/158 (2018). https://eprint.iacr.org/2018/158

CrossRef Google Scholar
Todo, Y.: Structural evaluation by generalized integral holding. In: Oswald, East., Fischlin, M. (eds.) EUROCRYPT 2015. LNCS, vol. 9056, pp. 287–314. Springer, Heidelberg (2015). https://doi.org/10.1007/978-three-662-46800-5_12

CrossRef Google Scholar
Todo, Y., Isobe, T., Hao, Y., Meier, W.: Cube attacks on not-blackbox polynomials based on division property. In: Katz, J., Shacham, H. (eds.) CRYPTO 2017. LNCS, vol. 10403, pp. 250–279. Springer, Cham (2017). https://doi.org/10.1007/978-3-319-63697-9_9

CrossRef Google Scholar
Wang, Ten., Yin, Y.Fifty., Yu, H.: Finding collisions in the full SHA-one. In: Shoup, 5. (ed.) CRYPTO 2005. LNCS, vol. 3621, pp. 17–36. Springer, Heidelberg (2005). https://doi.org/10.1007/11535218_2

CrossRef Google Scholar
Wang, X., Yu, H.: How to break MD5 and other hash functions. In: Cramer, R. (ed.) EUROCRYPT 2005. LNCS, vol. 3494, pp. nineteen–35. Springer, Heidelberg (2005). https://doi.org/10.1007/11426639_2

CrossRef Google Scholar

Download references

Acknowledgement

The authors would like to thank anonymous reviewers for their helpful comments. Nosotros likewise thank National Supercomputing Center in Wuxi for their back up of Sunway TaihuLight, which is the virtually powerful supercomputer. This piece of work was supported by the National Key Research and Development Program of China (Grant No. 2017YFA0303903), and National Cryptography Development Fund (No. MMJJ20170121), and Zhejiang Province Primal R&D Project (No. 2017C01062).

Writer information

Authors and Affiliations

Department of Calculator Science and Technology, Tsinghua Academy, Beijing, 100084, Mainland china

Ximing Fu
Institute for Advanced Report, Tsinghua Academy, Beijing, 100084, China

Xiaoyun Wang & Xiaoyang Dong
School of Mathematics, Shandong Academy, Jinan, 250100, China

Xiaoyun Wang
Primal Laboratory of Cryptologic Technology and Data Security, Ministry of Education, Shandong Academy, Jinan, 250100, China

Xiaoyun Wang
FHNW, Windisch, Switzerland

Willi Meier

Corresponding author

Correspondence to Xiaoyun Wang .

Editor information

Editors and Affiliations

The University of Texas at Austin, Austin, Texas, USA

Hovav Shacham
Georgia Institute of Technology, Atlanta, Georgia, USA

Alexandra Boldyreva

A The Details of Determining the Degree Upper Bound of Output for 721-round Trivium

For $z_{721}|_{\deg >36}=s_{ii}^{546}s_{ii}^{547}+s_{1}^{573}s_{1}^{574}$, the four state bits $s_{2}^{546}$, $s_{2}^{547}$, $s_{1}^{573}$, $s_{1}^{574}$ can be expressed using land bits furthermore. Substitute the four state bits using the expression and discard the land terms whose caste is lower than 37, then the resulted $z_{721}|_{\deg >36}=s_{1}^{463}s_{1}^{464}s_{one}^{478}+s_{one}^{464}s_{1}^{465}s_{ane}^{477}+s_{0}^{481}s_{0}^{482}s_{0}^{508}+s_{0}^{482}s_{0}^{483}s_{0}^{507}+s_{0}^{482}s_{0}^{483}s_{1}^{495}+s_{0}^{481}s_{0}^{482}s_{1}^{496}$. Then the state bits involved in the polynomial can exist expressed using state bits, and then that we can obtain $z_{721}|_{\deg >36}=s_{0}^{412}s_{2}^{372}s_{ii}^{373}s_{2}^{398}s_{2}^{399}+s_{0}^{413}s_{2}^{371}s_{2}^{372}s_{ii}^{398}s_{2}^{399}+s_{0}^{413}s_{2}^{373}s_{two}^{374}s_{2}^{397}s_{ii}^{398}+$ $s_{0}^{414}s_{2}^{372}s_{2}^{373}s_{two}^{397} s_{2}^{398}+s_{0}^{403}s_{0}^{404}s_{2}^{372}s_{2}^{373}s_{ii}^{417}+s_{0}^{403}s_{0}^{404}$ $s_{2}^{373}s_{2}^{374}s_{2}^{416}+s_{0}^{403}s_{0}^{404}$ $s_{2}^{372}s_{ii}^{373}s_{2}^{374}+s_{0}^{403}s_{0}^{404}s_{2}^{371} s_{2}^{373}s_{2}^{374}+s_{0}^{403}s_{0}^{404}s_{0}^{413}s_{2}^{373}s_{2}^{374}+s_{0}^{403}s_{0}^{404}s_{0}^{414}s_{ii}^{372}s_{2}^{373}+$ $s_{0}^{404}s_{0}^{405}s_{2}^{371}s_{2}^{372}s_{2}^{416}+s_{0}^{404}s_{0}^{405}s_{2}^{372}s_{ii}^{373}s_{2}^{415}+s_{0}^{404}s_{0}^{405}s_{two}^{371}s_{two}^{372}s_{2}^{373}+s_{0}^{404}s_{0}^{405}s_{two}^{370}$ $s_{2}^{372}s_{ii}^{373}+s_{0}^{404}s_{0}^{405}s_{0}^{412}s_{two}^{372}s_{2}^{373} +s_{0}^{404}s_{0}^{405}s_{0}^{413}s_{2}^{371}s_{two}^{372}$.

Echo the process above and nosotros tin obtain $z_{721}|_{\deg >36}=s_{1}^{290}s_{1}^{291}s_{i}^{305}s_{2}^{293}$ $s_{2}^{294}s_{2}^{295}s_{2}^{303}s_{2}^{304}+s_{1}^{291}s_{i}^{292}s_{1}^{304}s_{2}^{293}s_{two}^{294}s_{2}^{295}s_{2}^{303}s_{2}^{304}+s_{1}^{290}s_{one}^{291}s_{1}^{292}s_{ii}^{293} s_{ii}^{294}s_{ii}^{295}s_{2}^{303}$ $s_{2}^{304}+s_{ane}^{289}s_{1}^{291}s_{1}^{292}s_{2}^{293}s_{2}^{294}s_{ii}^{295}s_{ii}^{303}s_{2}^{304}+s_{1}^{291}s_{i}^{292}s_{2}^{286}s_{2}^{293}s_{2}^{294}s_{2}^{295}s_{two}^{303} s_{2}^{304}+s_{one}^{290}$ $s_{i}^{291}s_{two}^{287}s_{two}^{293}s_{2}^{294}s_{ii}^{295}s_{2}^{303}s_{2}^{304}+s_{1}^{290}s_{ane}^{291}s_{1}^{305}s_{ii}^{292}s_{two}^{294}s_{two}^{295}s_{two}^{303}s_{2}^{304}+s_{1}^{291} s_{1}^{292}s_{one}^{304}$ $s_{2}^{292}s_{2}^{294}s_{two}^{295}s_{2}^{303}s_{2}^{304}+s_{1}^{290}s_{one}^{291}s_{ane}^{292}s_{2}^{292}s_{ii}^{294}s_{2}^{295}s_{2}^{303}s_{two}^{304}+s_{one}^{289}s_{1}^{291}s_{one}^{292}s_{two}^{292}s_{2}^{294}s_{2}^{295}$ $s_{2}^{303}s_{2}^{304}+s_{1}^{291} s_{1}^{292}s_{two}^{286}s_{2}^{292}s_{2}^{294}s_{2}^{295}s_{2}^{303}s_{two}^{304}+s_{one}^{290}s_{1}^{291}s_{2}^{287}s_{2}^{292}s_{2}^{294}s_{2}^{295}s_{two}^{303}s_{2}^{304}+$ $s_{ane}^{289}s_{1}^{290}s_{1}^{304}s_{2}^{293}s_{two}^{294}s_{2}^{295}s_{2}^{304}s_{two}^{305}+s_{one}^{290}s_{1}^{291}s_{1}^{303}s_{2}^{293}s_{2}^{294}s_{2}^{295}s_{2}^{304}s_{2}^{305}+s_{1}^{289}s_{1}^{290}s_{i}^{291}$ $s_{2}^{293}s_{2}^{294}s_{two}^{295}s_{2}^{304}s_{2}^{305}+s_{1}^{288}s_{1}^{290}s_{i}^{291}s_{2}^{293}s_{2}^{294}s_{2}^{295}s_{2}^{304}s_{two}^{305}+s_{1}^{290}s_{1}^{291}s_{2}^{285}s_{two}^{293}s_{2}^{294}s_{2}^{295}$ $s_{ii}^{304}s_{2}^{305}+s_{1}^{289}s_{1}^{290}s_{2}^{286}s_{2}^{293}s_{2}^{294}s_{two}^{295}s_{2}^{304}s_{2}^{305}+s_{ane}^{289}s_{1}^{290}s_{i}^{304}s_{ii}^{292}s_{2}^{294}s_{ii}^{295}s_{2}^{304}s_{2}^{305}+$ $s_{ane}^{290}s_{1}^{291}s_{1}^{303}s_{ii}^{292}s_{2}^{294}s_{ii}^{295}s_{2}^{304}s_{2}^{305}+s_{i}^{289}s_{1}^{290}s_{one}^{291}s_{ii}^{292}s_{2}^{294}s_{2}^{295}s_{2}^{304}s_{two}^{305}+s_{1}^{288}s_{one}^{290}s_{1}^{291}$ $s_{2}^{292}s_{ii}^{294}s_{2}^{295}s_{2}^{304}s_{two}^{305}+s_{1}^{290}s_{i}^{291}s_{two}^{285}s_{2}^{292}s_{2}^{294}s_{2}^{295}s_{two}^{304}s_{2}^{305}+s_{i}^{289}s_{1}^{290}s_{two}^{286}s_{2}^{292}s_{ii}^{294}s_{two}^{295}$ $s_{2}^{304}s_{2}^{305}+s_{1}^{289}s_{ane}^{290}s_{i}^{304}s_{2}^{294}s_{two}^{295}s_{two}^{296}s_{2}^{302}s_{2}^{303}+s_{1}^{290}s_{1}^{291}s_{1}^{303}s_{two}^{294}s_{2}^{295}s_{2}^{296}s_{2}^{302}s_{2}^{303}+$ $s_{1}^{289}s_{one}^{290}s_{ane}^{291}s_{2}^{294}s_{2}^{295}s_{2}^{296}s_{2}^{302}s_{2}^{303}+s_{1}^{288}s_{1}^{290}s_{i}^{291}s_{2}^{294}s_{2}^{295}s_{ii}^{296}s_{2}^{302}s_{2}^{303}+s_{one}^{290}s_{1}^{291}s_{2}^{285}$ $s_{ii}^{294}s_{2}^{295}s_{2}^{296}s_{2}^{302}s_{2}^{303}+s_{1}^{289}s_{1}^{290}s_{2}^{286}s_{2}^{294}s_{2}^{295}s_{2}^{296}s_{ii}^{302}s_{2}^{303}+s_{1}^{289}s_{ane}^{290}s_{ane}^{304}s_{2}^{293}s_{two}^{295}s_{2}^{296}$ $s_{ii}^{302}s_{2}^{303}+s_{1}^{290}s_{1}^{291}s_{1}^{303}s_{2}^{293}s_{2}^{295}s_{2}^{296}s_{2}^{302}s_{2}^{303} +s_{1}^{289}s_{1}^{290}s_{1}^{291}s_{2}^{293}s_{2}^{295}s_{2}^{296}s_{2}^{302}s_{2}^{303}+$ $s_{ane}^{288}s_{1}^{290}s_{1}^{291}s_{ii}^{293}s_{2}^{295}s_{two}^{296}s_{2}^{302}s_{2}^{303}+s_{i}^{290}s_{one}^{291}s_{ii}^{285}s_{2}^{293}s_{two}^{295}s_{two}^{296}s_{2}^{302}s_{two}^{303}+s_{1}^{289}s_{1}^{290}s_{2}^{286}$ $s_{2}^{293}s_{2}^{295}s_{two}^{296}s_{2}^{302}s_{2}^{303}+s_{1}^{288}s_{ane}^{289}s_{1}^{303}s_{2}^{294}s_{2}^{295}s_{two}^{296}s_{2}^{303}s_{ii}^{304}+s_{1}^{289}s_{1}^{290}s_{1}^{302}s_{2}^{294}s_{ii}^{295}$ $s_{2}^{296}s_{2}^{303}s_{ii}^{304}+s_{1}^{288}s_{i}^{289}s_{1}^{290}s_{2}^{294}s_{2}^{295}s_{2}^{296}s_{two}^{303}s_{2}^{304}+s_{1}^{287}s_{i}^{289}s_{1}^{290}s_{2}^{294}s_{2}^{295}s_{2}^{296}s_{2}^{303}$ $s_{2}^{304}+s_{1}^{289}s_{i}^{290}s_{2}^{284}s_{ii}^{294}s_{two}^{295}s_{2}^{296}s_{2}^{303}s_{two}^{304}+s_{1}^{288}s_{1}^{289}s_{two}^{285}s_{2}^{294}s_{2}^{295}s_{2}^{296}s_{2}^{303}s_{2}^{304} +s_{i}^{288}$ $s_{1}^{289}s_{1}^{303}s_{2}^{293}s_{2}^{295}s_{ii}^{296}s_{2}^{303}s_{2}^{304}+s_{i}^{289}s_{1}^{290}s_{i}^{302}s_{2}^{293}s_{ii}^{295}s_{2}^{296}s_{2}^{303}s_{2}^{304}+s_{i}^{288}s_{i}^{289}s_{1}^{290}s_{2}^{293}$ $s_{2}^{295}s_{ii}^{296}s_{ii}^{303}s_{2}^{304}+s_{ane}^{287}s_{one}^{289}s_{i}^{290}s_{2}^{293}s_{ii}^{295}s_{ii}^{296}s_{2}^{303}s_{2}^{304}+s_{1}^{289}s_{1}^{290}s_{2}^{284}s_{2}^{293}s_{2}^{295}s_{ii}^{296}s_{2}^{303}$ $s_{ii}^{304}+s_{1}^{288}s_{1}^{289}s_{ii}^{285}s_{ii}^{293}s_{2}^{295}s_{2}^{296}s_{2}^{303}s_{2}^{304}$.

Substitute once more and at that place remains no land term, so that the caste of $z_{721}$ is lower than 37, which can be derived as distinguishers with lower complexity.

Rights and permissions

Copyright information

Almost this paper

Verify currency and authenticity via CrossMark

Cite this paper

Fu, 10., Wang, X., Dong, 10., Meier, W. (2018). A Key-Recovery Attack on 855-round Trivium. In: Shacham, H., Boldyreva, A. (eds) Advances in Cryptology – CRYPTO 2018. CRYPTO 2018. Lecture Notes in Reckoner Science(), vol 10992. Springer, Cham. https://doi.org/10.1007/978-iii-319-96881-0_6

Download citation

.RIS
.ENW
.BIB

DOI : https://doi.org/10.1007/978-iii-319-96881-0_6
Published: 24 July 2018
Publisher Proper noun: Springer, Cham
Impress ISBN: 978-3-319-96880-3
Online ISBN: 978-3-319-96881-0
eBook Packages: Computer science Information science (R0)